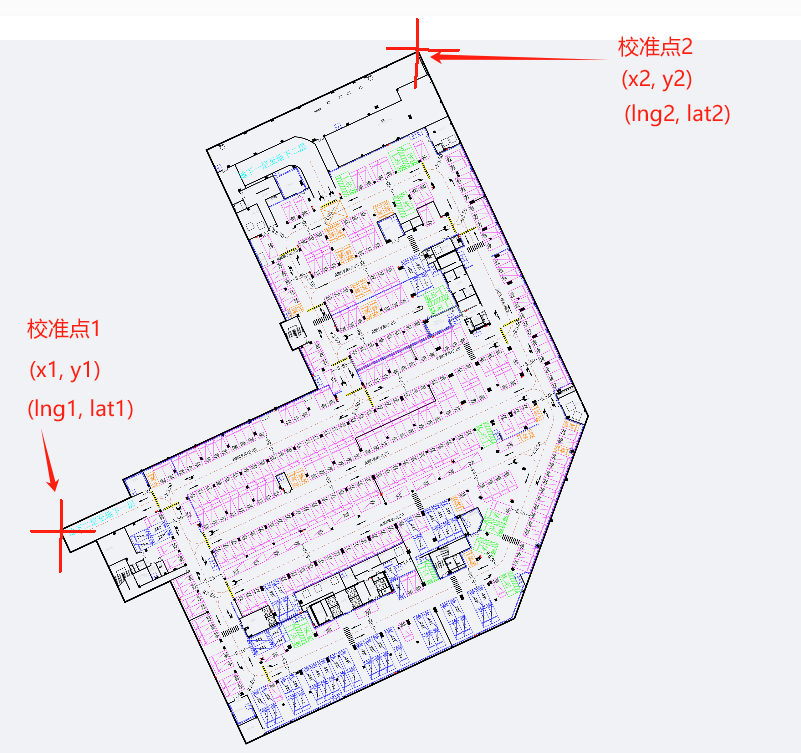
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
| import proj4 from 'proj4'
const firstProjection =
'PROJCS["CGCS2000 / 3-degree Gauss-Kruger CM 120E",GEOGCS["China Geodetic Coordinate System 2000",DATUM["China_2000",SPHEROID["CGCS2000",6378137,298.257222101,AUTHORITY["EPSG","1024"]],AUTHORITY["EPSG","1043"]],PRIMEM["Greenwich",0,AUTHORITY["EPSG","8901"]],UNIT["degree",0.0174532925199433,AUTHORITY["EPSG","9122"]],AUTHORITY["EPSG","4490"]],PROJECTION["Transverse_Mercator"],PARAMETER["latitude_of_origin",0],PARAMETER["central_meridian",120],PARAMETER["scale_factor",1],PARAMETER["false_easting",500000],PARAMETER["false_northing",0],UNIT["metre",1,AUTHORITY["EPSG","9001"]],AUTHORITY["EPSG","4549"]]';
const secondProjection =
'GEOGCS["WGS 84",DATUM["WGS_1984",SPHEROID["WGS 84",6378137,298.257223563,AUTHORITY["EPSG","7030"]],AUTHORITY["EPSG","6326"]],PRIMEM["Greenwich",0,AUTHORITY["EPSG","8901"]],UNIT["degree",0.0174532925199433,AUTHORITY["EPSG","9122"]],AUTHORITY["EPSG","4326"]]';
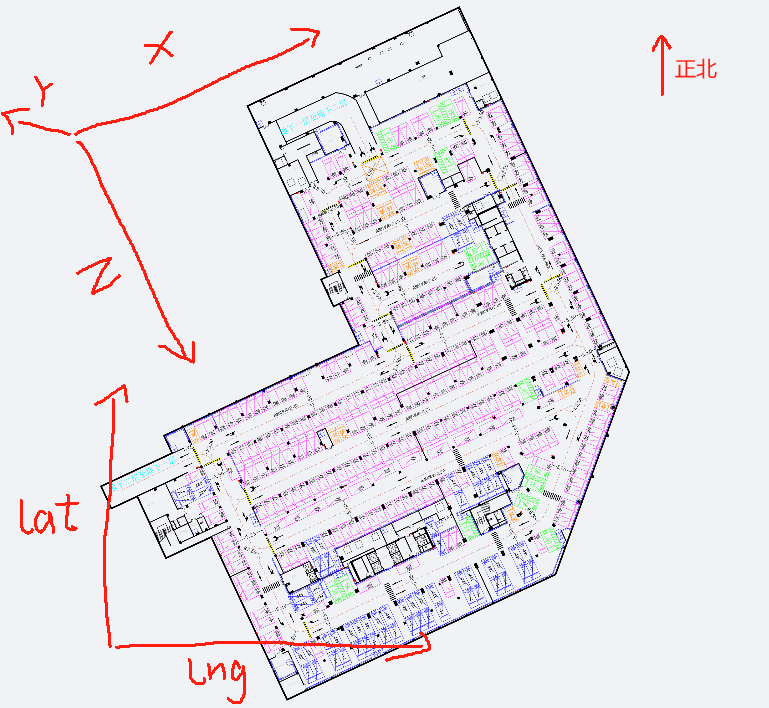
const fixLnglat0 = [121.31155131270114, 31.143545887099073];
const fixLnglat0 = [121.31155131270114, 31.143545887099073];
const fixLnglat1 = [121.31524160667905, 31.141933166985034];
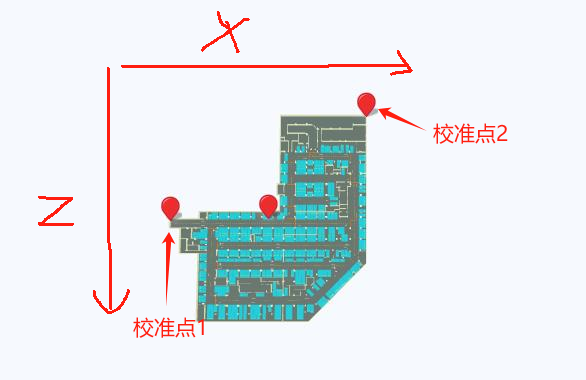
const fixXy0 = [4.43, 0, -43.95];
const fixXy1 = [28.37, 0, -12.75];
const angleDifference = calculateAngleDifference(fixLnglat0, fixLnglat1, fixXy0, fixXy1);
console.log("angleDifference", angleDifference);
const rotationTransX = (fixLnglat0, angleDifference) => {
const cosAngle = Math.cos(angleDifference);
const sinAngle = Math.sin(angleDifference);
return fixLnglat0[0] * cosAngle - fixLnglat0[1] * sinAngle;
}
const rotationTransY = (fixLnglat0, angleDifference) => {
const cosAngle = Math.cos(angleDifference);
const sinAngle = Math.sin(angleDifference);
return fixLnglat0[0] * sinAngle + fixLnglat0[1] * cosAngle;
}
const calculateLatLonToCoordRatio = (fixLnglat0, fixLnglat1, fixXy0, fixXy1, angleDifference) => {
const xy0 = proj4(secondProjection, firstProjection, fixLnglat0);
const xy1 = proj4(secondProjection, firstProjection, fixLnglat1);
const deltaLon1 = rotationTransX(xy1, angleDifference);
const deltaLon0 = rotationTransX(xy0, angleDifference);
const deltaLat1 = rotationTransY(xy1, angleDifference);
const deltaLat0 = rotationTransY(xy0, angleDifference);
const deltaLon = deltaLon1 - deltaLon0;
const deltaLat = deltaLat1 - deltaLat0;
const deltaX = fixXy1[0] - fixXy0[0];
const deltaZ = fixXy1[2] - fixXy0[2];
const ratioX = deltaX / deltaLon;
const ratioZ = deltaZ / deltaLat;
return { ratioX, ratioZ };
}
const latLonToThreeJsCoords = (lat, lon) => {
const xy = proj4(secondProjection, firstProjection, [lon, lat]);
const fixxy = proj4(secondProjection, firstProjection, fixLnglat0);
const deltaLon = rotationTransX(xy, angleDifference) - rotationTransX(fixxy, angleDifference);
const deltaLat = rotationTransY(xy, angleDifference) - rotationTransY(fixxy, angleDifference);
const {
ratioX,
ratioZ
} = calculateLatLonToCoordRatio(fixLnglat0, fixLnglat1, fixXy0, fixXy1, angleDifference);
console.log("ratioX", 1/ratioX);
const x = fixXy0[0] + ratioX * deltaLon;
const z = fixXy0[2] + ratioZ * deltaLat;
return [x, z];
}
const degreesToRadians = (degrees) => {
return degrees * Math.PI / 180;
}
const calculateBearing = (lat0, lon0, lat1, lon1) => {
const lat0Rad = degreesToRadians(lat0);
const lon0Rad = degreesToRadians(lon0);
const lat1Rad = degreesToRadians(lat1);
const lon1Rad = degreesToRadians(lon1);
const dLon = lon1Rad - lon0Rad;
const y = Math.sin(dLon) * Math.cos(lat1Rad);
const x = Math.cos(lat0Rad) * Math.sin(lat1Rad) - Math.sin(lat0Rad) * Math.cos(lat1Rad) * Math.cos(dLon);
const bearing = Math.atan2(y, x);
return bearing;
}
const calculateAngleDifference = (fixLnglat0, fixLnglat1, fixXy0, fixXy1) => {
const lat0 = fixLnglat0[1];
const lon0 = fixLnglat0[0];
const lat1 = fixLnglat1[1];
const lon1 = fixLnglat1[0];
const bearing = calculateBearing(lat0, lon0, lat1, lon1);
const deltaX = fixXy1[0] - fixXy0[0];
const deltaZ = fixXy1[2] - fixXy0[2];
const angleWithZ = Math.atan2(deltaX, -deltaZ) * (180 / Math.PI);
const angleDifference = bearing - Math.atan2(deltaX, -deltaZ);
return angleDifference;
}
const lat = 31.142235878203852;
const lon = 121.31308429914422;
const threeJsCoords = latLonToThreeJsCoords(lat, lon);
|